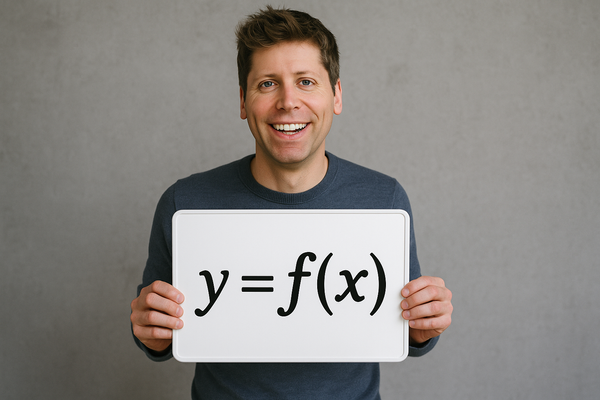#001: The Function That Started It All

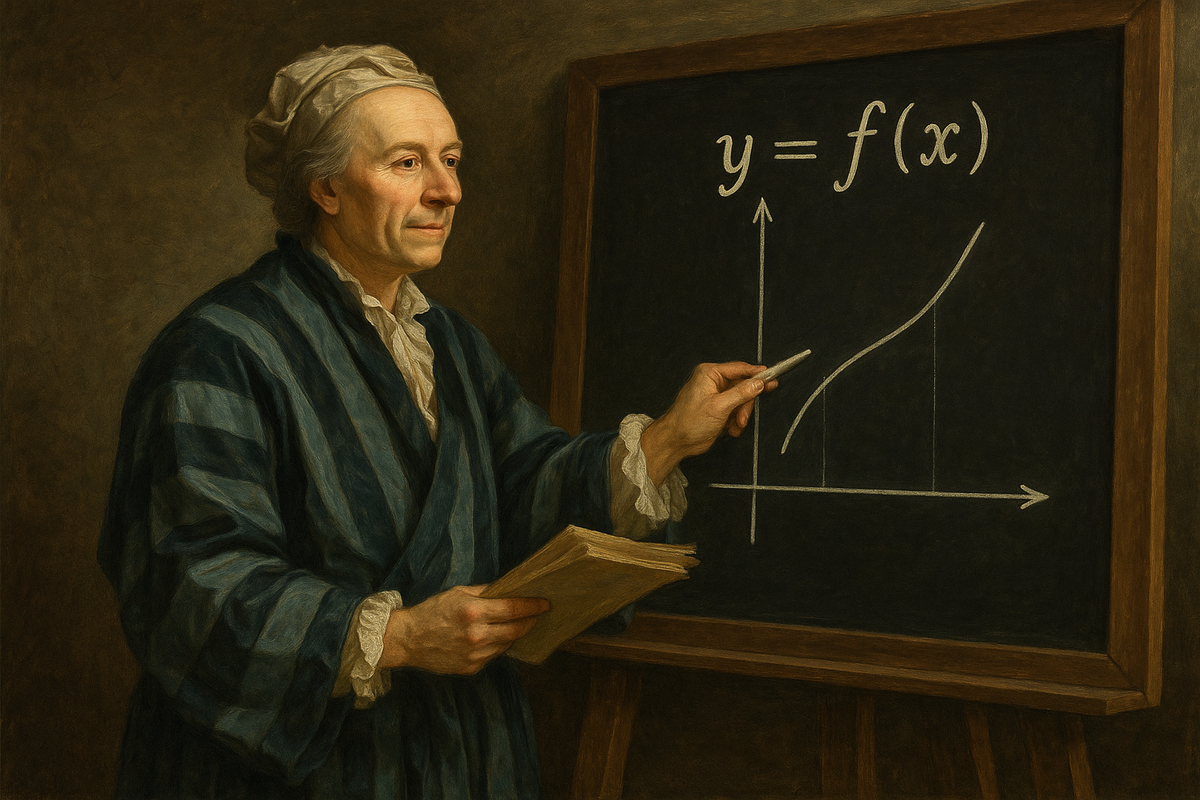
In the world of mathematics, few notations are as elegant, compact, and profound as this: y = f(x). On the surface, it's a simple expression. But beneath that simplicity lies a revolutionary idea that changed not just math, but how we think about systems, logic, and even the way machines learn. This is our homage to the formula that inspired our name—and to the man who first wrote it down.

The Birth of a Formula

In the 18th century, the legendary Swiss mathematician Leonhard Euler introduced the function notation f(x). While functions themselves had been studied before Euler, it was his elegant formulation that brought clarity to the relationship between inputs and outputs. With this single expression, Euler offered a universal language for transformation:

• x is the input
• f is the function that processes the input
• y is the resulting output

Whether you're calculating a trajectory, modeling a system, or solving a real-world problem, y = f(x) is a way of expressing cause and effect, action and result.

"Mathematics is the art of giving the same name to different things." — Henri Poincaré

And nowhere is that more true than with y = f(x).

What It Really Means

At its heart, y = f(x) is a statement of transformation. You take something (x), apply a process to it (f), and get something new (y). It’s a framework we use every day, often without realizing it:

• Blender: x = fruit, f = blending, y = smoothie
• Resume Screening AI: x = resume, f = model logic, y = hire/no-hire signal
• Weather App: x = atmospheric data, f = prediction algorithm, y = forecast

This formula doesn’t just live on chalkboards. It lives in kitchens, inboxes, news feeds, hospitals, and financial markets. It’s the underlying idea behind how we build, measure, and improve systems.

From Functions to Artificial Intelligence

In AI, y = f(x) becomes literal. Here’s how:

• x is your raw data — text, numbers, images, audio.
• f is the model — a function that has been trained to understand patterns in the data.
• y is the prediction — the output that the model gives you.

For example:

• Feed in a sentence (x), the model (f) predicts sentiment (y).
• Feed in a series of stock prices (x), the model (f) predicts the next price (y).
• Feed in your voice (x), the model (f) identifies you (y).

In every case, AI is applying some function to your input to generate an output—just as Euler envisioned, only now with a few billion more parameters.

Why We Chose This Name

We chose y = f(x) as our identity because it reflects our philosophy:

• Clarity over complexity — great ideas should be understandable.
• Process over mystique — AI is not magic; it's math and logic.
• Transformation at the core — every post here is an f transforming x into insight.

Just like Euler simplified complexity with f(x), we aim to do the same for artificial intelligence.

A Thank You to Euler

Euler may not have envisioned deep learning or generative models, but he gave us a blueprint for thinking in systems. For defining transformations. For understanding that what we put in—and how we process it—determines what comes out.

To him, f(x) was just good math. To us, it’s a mission.

Stay tuned. The next function is just getting started.

– Sandeep Pamulaparthi & Laxmi Nanditha Vijay
Founders, yequalsfofx.com