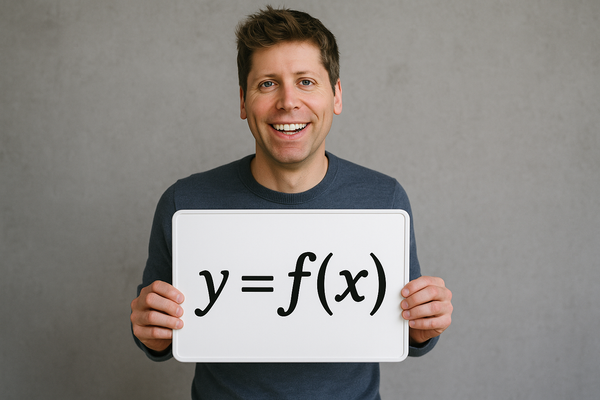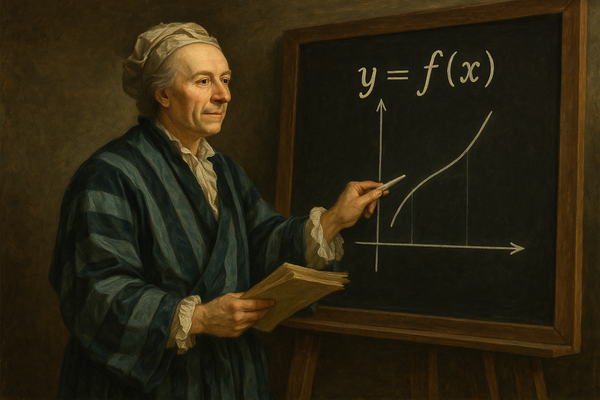#004: Decision Trees: Learning to Decide, One Branch at a Time

Sandeep Pamulaparthi & Laxmi Nanditha Vijay

— 2 min read
#004: Decision Trees: Learning to Decide, One Branch at a Time
Onto a clean white canvas draw a very creative image of a tree with Acrylic colors

When we talk about machine learning, few concepts are as intuitive—and powerful—as the Decision Tree. Much like its name suggests, a decision tree maps choices and consequences in a way that is both human-readable and mathematically elegant. Through the lens of y = f(x), it becomes even easier to understand how decision trees transform inputs into outputs with simple, logical steps.

The Essence of a Decision Tree

At its heart, a decision tree is about answering a question: "Given what I know (x), what should I predict (y)?" A decision tree does this by splitting data into branches based on feature values until it reaches a prediction.

In y = f(x) terms:

  • x = The set of features (inputs) describing a situation.
  • f = The tree structure—a sequence of decisions based on those features.
  • y = The final prediction: a class label, a number, or a probability.
Think of the tree as the function "f" that applies a series of 'if-then' tests to x, leading to a decision y.

How a Decision Tree Works: Should You Approve a Loan?

Imagine you're building a decision tree to decide whether to approve a loan application. Your features (x) might include:

  • Credit Score (Good, Average, Poor)
  • Income Level (High, Medium, Low)
  • Loan Amount Requested (Small, Medium, Large)
  • Existing Debts (Yes, No)

The tree might start like this:

  1. Is Credit Score Good?
    • Yes → Approve loan.
    • No → Check Income Level.
  2. Is Income Level High?
    • Yes → Approve loan.
    • No → Check Existing Debts.
  3. Does the applicant have Existing Debts?
    • Yes → Reject loan.
    • No → Approve loan.

Visualization:

          [Credit Score]
          /            \
      Good              Bad
     (Approve)         [Income Level]
                        /         \
                    High           Low
                  (Approve)      [Existing Debts]
                                 /            \
                               Yes            No
                            (Reject)       (Approve)

Input (x):

  • Credit Score = Bad
  • Income Level = Low
  • Existing Debts = No

Function (f):

  • Step 1: Credit Score = Bad ➔ Go to Income Level.
  • Step 2: Income Level = Low ➔ Check Existing Debts.
  • Step 3: Existing Debts = No ➔ Approve the loan.

Output (y):

  • Decision = Approve Loan

This example clearly shows how simple, logical steps lead from features to outcomes in a decision tree, following the y = f(x) framework.

Simple inputs, sequential logic, actionable output—all modeled perfectly by y = f(x).

Strengths of Decision Trees

  • Interpretability: Humans can understand the decisions easily.
  • Flexibility: Can handle both categorical and numerical data.
  • Non-linear Boundaries: Unlike linear models, trees can capture complex patterns.
  • Versatility: Used for classification, regression, and even ranking problems.

Weaknesses (and How to Improve)

  • Overfitting: Deep trees can memorize the training data too closely.
  • Instability: Small changes in data can lead to different trees.

Solutions?

  • Pruning the tree to avoid over-complexity.
  • Ensembling multiple trees (like in Random Forests or Gradient Boosted Trees) to create more robust models.

Why Decision Trees Matter in AI

Decision trees remind us that sophisticated predictions often emerge from simple, sequential logic. They are one of the building blocks of modern AI ensembles and feature in critical applications like:

  • Medical diagnoses
  • Fraud detection
  • Loan approvals
  • Image classification

When you boil down these applications, you see it: a stream of features (x), flowing through carefully learned decisions (f), resulting in informed outcomes (y).

Closing Thoughts

Through the lens of y = f(x), a decision tree is simply a dynamic function—a living map of "if-then" transformations that guide data from uncertainty to clarity.

Every split, every branch, every leaf is another reminder: intelligence, whether human or artificial, often begins by asking the right questions.

Until next time, keep planting better trees in your models—and in your thinking.

– Sandeep Pamulaparthi & Laxmi Nanditha Vijay
Founders, yequalsfofx.com

Read more